 Physics classes in high school are taught in such a way as to have a balance between the kinetic and the potential energy of a motive object in a “fixed system” at a given “fixed moment” in time. We then look at the continuation of kinetic energy and the release of potential energy to determine what changes take place upon reaching a later “fixed system”, at a later “fixed moment” in time in after an arbitrary “interval”. By comparing the change in the “fixed systems” at two different “fixed moments”, we can make a generalization or guess about what the subsequent “fixed system” will look like upon completion of the subsequent “interval” leading to the next “fixed moment” (the third time is the charm). If we can perform this calculation before the interval takes place, by using all our powers of observation and calculation, we can know what is going to happen before it ever takes place!
These objects can all be made from different materials, so in order to accurately predict the values, the experiment must be performed in all combinations of materials in order to reliably predict the outcome of an imaginary experiment with some arbitrary block, ramp, and air collection. That’s because the block, ramp, and air could all be made from different types of solids, liquids, and gasses on the periodic table. Since phase states of matter (such as solids, liquids, and gasses) can be converted between the different states with chemical and physical and mathematical operations, it is best to treat each type of phase state of matter as different and unique, even if you believe them to be different phases of a single element of matter on the periodic table.
In other words, you can cool vapor H2O into liquid H2O, and cool liquid H2O into solid H2O; you can heat solid H2O into liquid H2O, and heat liquid H2O into vapor H2O; and you can mix solid H2O, liquid H2O, and vapor H2O into suspensions of two or more different kinds of H2O. But what is really happening? Are all of these different forms of matter really the same things, or is H2O getting turned into two DIFFERENT things?
When looking at suspensions of H2O, it is best to remember that they are just “air”, “water”, and “ice” mixed up to create different things. Here are just a few of the different things we can see from combinations of all three “phase states” of H2O:
Ice water – has medium amounts of cubes of ice, that are floating in lots of water, and have very low amounts of air on top (It’s a good preparation to drink in a cup!)
Snow – has medium amounts of little pieces of ice, has no water, and is falling in between lots of air (It’s a good method of layering H2O evenly over other things from above!)
Sleet – has medium amounts of little pieces of ice, and they are coated in little droplets of water, that are sometimes so heavy that they falling between lots of air, if the air is not dense enough (It’s a very fast method of layering H2O over other things from above, but not as evenly as snow!)
Black ice – has a lot of ice in a flat expanse, covered by a little layer of water, and covered again by a high pressure mound of very cold air (It’s a good surface for low friction ice skating, because everything has a lot of energy to work!).
Steam – has no ice, and little droplets of regular temperature water, that are being carried upwards by hot air.
We still might not know what will happen if the solids, liquids, and gasses are made from a different combination of elements, or what will happen if we find a new phases state of matter, like Jello (which is (solid-liquid)), or plasma (which is (liquid-gas)), or what will happen if we replace solid mediums of transmissions with liquid or gas ones (Or even Gels or Plasmas! Fruit cocktail Jello vs. Jello commercial on a Plasma TV?). Having understood the reason why we must be utilitarian and examine all those different states and types of matter as unique, let’s try to approximate the properties of a block, ramp, and air in one such system, using mathematical descriptions as best as we can:
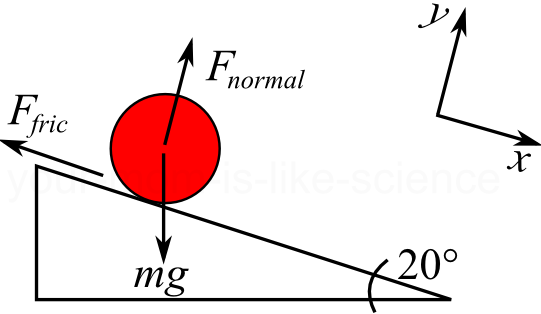
Consider, for example, a symettrical inclined plane with a [front, top, side]=[◉, > , >], upon which a block [front, top, side]=[O, O, O] is sliding, which are both getting narrower, shorter, and lower.
Depending on materials in the closed system, the regressions and progressions of mass of the different objects must also be taken into account, as interactions between the different parts turn the block into air and into ramp, turn the ramp into air and block, and turn the air into block and ramp.
Physics classes in high school are taught in such a way as to have a balance between the kinetic and the potential energy of a motive object in a “fixed system” at a given “fixed moment” in time. We then look at the continuation of kinetic energy and the release of potential energy to determine what changes take place upon reaching a later “fixed system”, at a later “fixed moment” in time in after an arbitrary “interval”. By comparing the change in the “fixed systems” at two different “fixed moments”, we can make a generalization or guess about what the subsequent “fixed system” will look like upon completion of the subsequent “interval” leading to the next “fixed moment” (the third time is the charm). If we can perform this calculation before the interval takes place, by using all our powers of observation and calculation, we can know what is going to happen before it ever takes place!
These objects can all be made from different materials, so in order to accurately predict the values, the experiment must be performed in all combinations of materials in order to reliably predict the outcome of an imaginary experiment with some arbitrary block, ramp, and air collection. That’s because the block, ramp, and air could all be made from different types of solids, liquids, and gasses on the periodic table. Since phase states of matter (such as solids, liquids, and gasses) can be converted between the different states with chemical and physical and mathematical operations, it is best to treat each type of phase state of matter as different and unique, even if you believe them to be different phases of a single element of matter on the periodic table.
In other words, you can cool vapor H2O into liquid H2O, and cool liquid H2O into solid H2O; you can heat solid H2O into liquid H2O, and heat liquid H2O into vapor H2O; and you can mix solid H2O, liquid H2O, and vapor H2O into suspensions of two or more different kinds of H2O. But what is really happening? Are all of these different forms of matter really the same things, or is H2O getting turned into two DIFFERENT things?
When looking at suspensions of H2O, it is best to remember that they are just “air”, “water”, and “ice” mixed up to create different things. Here are just a few of the different things we can see from combinations of all three “phase states” of H2O:
Ice water – has medium amounts of cubes of ice, that are floating in lots of water, and have very low amounts of air on top (It’s a good preparation to drink in a cup!)
Snow – has medium amounts of little pieces of ice, has no water, and is falling in between lots of air (It’s a good method of layering H2O evenly over other things from above!)
Sleet – has medium amounts of little pieces of ice, and they are coated in little droplets of water, that are sometimes so heavy that they falling between lots of air, if the air is not dense enough (It’s a very fast method of layering H2O over other things from above, but not as evenly as snow!)
Black ice – has a lot of ice in a flat expanse, covered by a little layer of water, and covered again by a high pressure mound of very cold air (It’s a good surface for low friction ice skating, because everything has a lot of energy to work!).
Steam – has no ice, and little droplets of regular temperature water, that are being carried upwards by hot air.
We still might not know what will happen if the solids, liquids, and gasses are made from a different combination of elements, or what will happen if we find a new phases state of matter, like Jello (which is (solid-liquid)), or plasma (which is (liquid-gas)), or what will happen if we replace solid mediums of transmissions with liquid or gas ones (Or even Gels or Plasmas! Fruit cocktail Jello vs. Jello commercial on a Plasma TV?). Having understood the reason why we must be utilitarian and examine all those different states and types of matter as unique, let’s try to approximate the properties of a block, ramp, and air in one such system, using mathematical descriptions as best as we can:
Consider, for example, a symettrical inclined plane with a [front, top, side]=[◉, > , >], upon which a block [front, top, side]=[O, O, O] is sliding, which are both getting narrower, shorter, and lower.
Depending on materials in the closed system, the regressions and progressions of mass of the different objects must also be taken into account, as interactions between the different parts turn the block into air and into ramp, turn the ramp into air and block, and turn the air into block and ramp.
I.a. Regressional Mass Measurement of Block, Ramp, and Air – Tracking the decay of the different elements in the fixed system:(((masses of block, ramp, and air at beginning of observation, M1(b), M1(r), M1(a)), (surface area of block, ramp, and air at beginning of observation, S1(b), S1(r), S1(a)), (contacted surface areas of block and air at beginning of observation, CBA1(b, a)), (contacted surface areas of block and ramp at beginning of observation, CBR1(b, r)), (contacted surface areas of air and ramp at beginning of observation, CAR1(a, r)), (porosity of block, ramp, and air at beginning of observation, (P1(b), P1(r), P1(a))), (density of block, ramp, and air at beginning of observation, (D1(b), D1(r), D1(a))), and (differences of mass, porosity, surface area, contacted surface, and density of block, ramp and air, (Δ(M1, M2), Δ(P1, P2), Δ(S1, S2), (Δ(CBA1, CBA2), Δ(CBR1,CBR2), Δ(CAR1, CAR2)), Δ(D1, D2)), between (time since first round of observation began, t(0), and time when observation ended, t(1) in time of a single round of observation, (T(t(0), t(x)))))) used to generate (rate of change coefficient of regressional friction of block, ramp, and air (F(b), F(r), F(a))). I.b. Progressional Mass Measurement of Block, Ramp, and Air – Tracking the growth of the different elements in the fixed system: (((masses of block, ramp, and air at beginning of observation M1(b), M1(r), M1(a)), (surface area of block, ramp, and air at beginning of observation, S1(b), S1(r), S1(a)), (contacted surface areas of block and air at beginning of observation, C1(b, a)), (contacted surface areas of block and ramp at beginning of observation, C1(b, r)), (contacted surface areas of air and ramp at beginning of observation, C1(a, r)), (porosity of block, ramp, and air at beginning of observation, (P1(b), P1(r), P1(a))), (density of block, ramp, and air at beginning of observation, (D1(b), D1(r), D1(a))), and (differences of mass, porosity, surface area, contacted surface, and density of block, ramp and air, (Δ(M1, M2), Δ(P1, P2)Δ, Δ(S1, S2), (Δ(CBA1, CBA2), Δ(CBR1,CBR2), Δ(CAR1, CAR2)), Δ(D1, D2)), between (time since first round of observation began, t(0), and (time when observation ended, t(1) in interval of a single round of observation, (T(t(0), t(x)))) used to generate (rate of change coefficient of progressional friction of block, ramp, and air , R(b), R(r), R(a))). The changes in mass can be simplified as ((Regressional Change ΔRM(m)) and (Progressional Change ΔPM(m))), once they are quantified by the observer. II.a.1. Horizontal Kinetic Energy of Block – The active movements of the block in the horizontal plane during an interval in the fixed system:(horizontal position of block H(b) between leftmost and rightmost bounds of ramp, R(l,r)), (mass of block, m(b)), (differences of change in position of block Δ(H(a), H(b)), (rate of change coefficient of regressional friction of block, ramp, and air (F(b), F(r), F(a)), (rate of change coefficient of progressional friction of block, ramp, and air , R(b), R(r), R(a)), in the (time since first round of observation began, t(0)), and (time when observation ended, t(x) in a single round of observation, ΔT(t(0), t(x))), used to generate (horizontal force vector of block, H(b)).
II.b.1.Vertical Kinetic Energy of Block – The active movements of the bock in the vertical plane during an interval in the fixed system:(vertical position of block H(b) between uppermost and lowermost bounds of ramp, R(u, l)), (mass of block, m(b)), (differences of change in position of block Δ(V(a), V(b)), (rate of change coefficient of regressional friction of block, ramp, and air (F(b), F(r), F(a)), (rate of change coefficient of progressional friction of block, ramp, and air , R(b), R(r), R(a)), in (time since first round of observation began, t(0), and (time when observation ended, t(x) in a single round of observation, ΔT(t(0), t(x))), used to generate (vertical force vector of block, V(b)).
II.c.1. Depth Kinetic Energy of Block – The active movements of the block in the depth plane during an interval in the fixed system: (depth position of block D(b) between furthestmost and closestmost bounds of ramp, R(f, c)), (mass of block, m(b)), (differences of change in position of block Δ(D(a), V(b)), (rate of change coefficient of regressional friction of block, ramp, and air (F(b), F(r), F(a)), (rate of change coefficient of progressional friction of block, ramp, and air , R(b), R(r), R(a)), in (time since first round of observation began, t(0)), and (time when observation ended, t(x) in a single round of observation, ΔT(t(0), t(x))), used to generate (depth force vector of block, D(b)).
II.d.1. Rotational Kinetic Force of Block – The summation of changes in horizontal, vertical, and depth movements of the block during an interval in the fixed system: Δ(H(B)1, H(B)2), Δ(V(B)1, V(B)2), Δ(D(B)1, D(B)2) To get the same desired kinetic forces for the ramp (II.a.2., II.b.2, II.c.2, II.d.2)and air (II.a.3., II.b.3, II.c.3, II.d.3), perform the same function with ramp in place of block (cycling the remaining two constants), and air in place of block (cycling the remaining two constants) in the above descriptions of section II.. III. Potential Energy of Mass of Block, Ramp, and Air – The places which the masses of block, ramp, and air can possibly be before the next interval terminates: (mass of block, ramp, and air M(b), M(r), M(a)), (force of gravitational acceleration of block, ramp, and air, G(b), G(r), G(a)), normal force of block, ramp, and air, N(b), N(r), N(a)), (location of point of contact between block and ramp in horizontal, vertical, depth, and rotational positions of block, LBR(Δ(h1, h2)1, Δ(v1, v2)1, Δ(d1, d2)1, Δ(r1, r2)1)), used to generate (location of center of mass of block and ramp C(b, r)), (location of point of contact between block and air in horizontal, vertical, depth, and rotational positions of block, LBA(Δ(h1, h2)2, Δ(v1, v2)2, Δ(d1, d2)2, (r1, r2)2)), used to generate (location of center of mass of block and air C(b, a)), (location of point of contact between ramp and air in horizontal, vertical, depth, and rotational positions of block, LRA(Δ(h1, h2)3, Δ(v1, v2)3, Δ(d1, d2)3, Δ(r1, r2)3), used to generate (location of center of mass of ramp and air, C(r, a)). The above description of potential energies is mostly a summary, and can be refactored to look like the kinetic energies (that is, having one “Wall of functions” for each object) through the process of breaking down the Δ (“Delta) functions into differeces and singularizing the functions. Doing so would make for better testability and insertion of equations into a computer simulation. IV.a. Total Energy of Block:total energy of block (TB(potential energy of block PE(b) and kinetic energy of block KE(b)) IV.b. Total Energy of Ramp: total energy of ramp (TR(potential energy of ramp PE(r) and kinetic energy of ramp KE(r)) IV.c. Total Energy of Air: total energy of air (TA(potential energy of air PE(a) and kinetic energy of air KE(a)) V. Total Energy of System: total energy of block, ramp, and air TE(TB, TR, TA) P.S. – I hate parenthesis. They are so visually difficult. Let me know if you have a better way of displaying mathematical sets of equations and orders of operation that is more comprehensible. P.P.S. – Suggested Listening: The Hives – The Black and White Album – Fall is Just Something Grown Ups Invented My own lyrics for the tune:
“I walked on this path for 500 or ten. It all got so fast, I could not see the end. The way back was steep, and the wind was my friend. It blew the wrong way, but I like to pretend.” P.P.P.S. – Suggested Reading: A post I wrote on G+ describing how to get ahead with it (Nerd Baller Secure Computer for Predicting the Future)P.P.P.P.S. – If you’re just a piss-poor college grad student, just do it with Shiner Bock and a rock instead a ball and a block. P.P.P.P.S. – The experiment can be generalized further by varying angles of the ramp; varying different masses of the ball, ramp, and air matter; constricting or expanding the air, ramp, and block into different volumes (constriction and expansion usually to be avoided, for safety of all involved, PV=nRT, according to my high school chemistry teacher, but thats only with well-measured and high quality ingredients and systems, and neglects to take into account all possible variations of all elements of matter (Suggested Reading: Wikipedia’s Article on (((P)(V))=((n)(R)(T))), the “Ideal Gas Law”), just like P=e^(Rt) (completely different equation dealing with statistical model growth, that while seeming unrelated due to the overlapping definitional qualities of the used variabless, still pertains to this study’s goals of tracking ALL manners and modes of regressional and progressional mass. Copy the equation from this site, and paste it into Wikipedia to find out more…); and varying the elemental uniposition or composition of the air, block, and ramp.

[…] database-powered, mathematically-simulated, metered-machined environments are able to perform: http://www.renaissancemusings.com/p-e/ You could install a 3D monitor and use a bi-visual 3D camera with HDMI/Wireless/USB […]
[…] and scans to highest grade levels ( Difference Engine for Space Movement Without Interaction Difference Engine for Prediction Summation A Difference Engine for Prediction Summation […]
[…] Suggested reading: P.E. : Physics Education […]